斜率优化入门

通过一道简单的例题入门斜率优化 Qwq。

任务安排2

给定 $n$ 个有 $T_i$、$C_i$ 两属性的机器和 $S$，将其分为若干段，第 $j$ 个段 $[l, r]​$ 的费用为

$$(sC_r - sC_{l - 1})\times(S \times j + sT_r)$$

$sC_i$，$sT_i$ 为前缀和数组，求最小费用。

$1 \le N \le 3 \times 10^5, \ \ 1 \le S, \ T_i , \ C_i \le 512$

推dp

以下的 $C​$，$T​$ 数组皆为前缀和处理后的数组。

设 $F_{i,j}$ 表示前 $i$ 个机器分 $j$ 段的最小费用，枚举最后一段的开头 $k$，易得转移：

$$F_{i,j}=\min_{1\le k < i}(F_{k,j-1} + (C_i - C_{k})\times(S \times j + T_i))$$

最暴力的方程。将段产生的费用分出来，每次计算当前这一段对后面的费用影响，即费用提前计算思想，可以优化掉第二维：

$$F_i= \min_{1\le j < i}(F_j + (C_i-C_j)\times T_i + (C_n-C_j) \times S)$$

这样可以达到 $\Theta(n^2)$ 的时间复杂度，对于本题的数据范围显然是不可行的，我们要对它进行优化废话。

对于这个式子，发现它同时包含了与 $i$、$j$ 相关的项（$C_j \times T_i$），比较不好处理，这时就要用到斜率优化了。

鬼知道是怎么想到的

斜率优化

将上面的式子进一步展开：

$$F_i=\min_{1\le j < i}(F_j + C_i\times T_i - C_j \times T_i + C_n \times S - C_j \times S)$$

与 $j$ 无关的可以提到左边：

$$F_i -C_i \times T_i - C_n \times S = \min_{1 \le j < i}(F_j - C_j \times T_i - C_j \times S)$$

即

$$F_i - C_i \times T_i - C_n \times S = \min_{1 \le j < i}(F_j - (T_i + S)\times C_j)$$

类比一次函数 $y=kx + b$，变为 $b = y - kx$，那么就可以这样设：

$$B_j = F_i - C_i \times T_i - C_n \times S \\ Y_j = F_j \\ K_j = T_i + S \\ X_j = C_j$$

这就是一条以 $T_i + S$ 为斜率，$F_i - C_i \times T_i - C_n \times S$ 为截距的直线（截距就是一次函数的 $b$）。

$C_i \times T_i$ 和 $C_n \times S$ 都是已知量，不会改变，所以求 $F_i$ 的最小值就是找到一个合适的 $j$，使截距最小化。

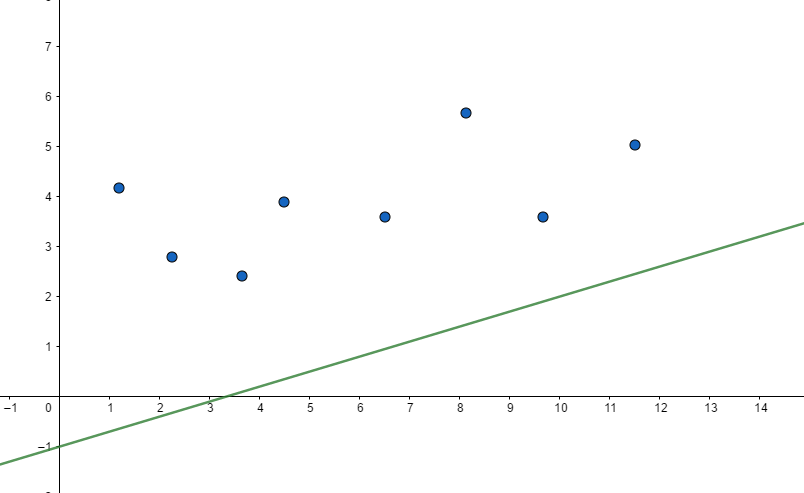
看着这个图考虑这样一个过程：一根斜率已知的直线 $i$，从下向上平移，遇到第一个点 $j(C_j, F_j)$ ，时此时截距即为最小值，like this：

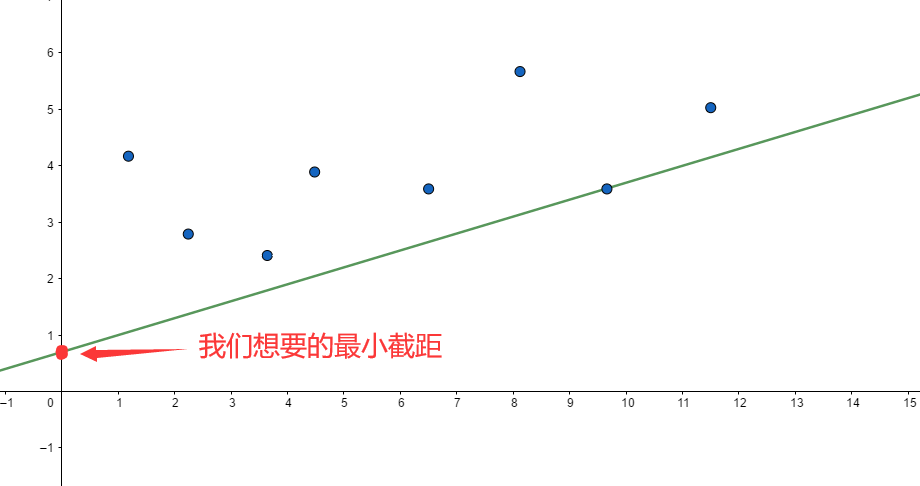
显然这样的决策点 $(C_j,F_j)$ 一定在下凸壳上（下凸壳：相邻两点连线斜率单调上升的若干个点），这个很容易从图形上直观理解，就不证明了。

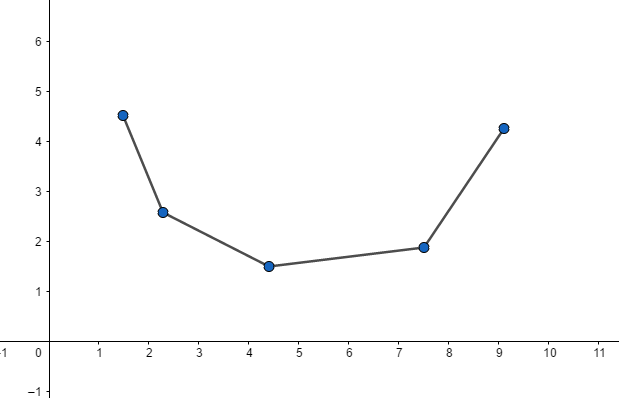
这就是一个下凸壳。那哪个点才是我们想要的决策点呢？显然，当直线与凸壳相交时交点左边的斜率都小于直线斜率，右边都大于直线斜率，看图就很好理解：

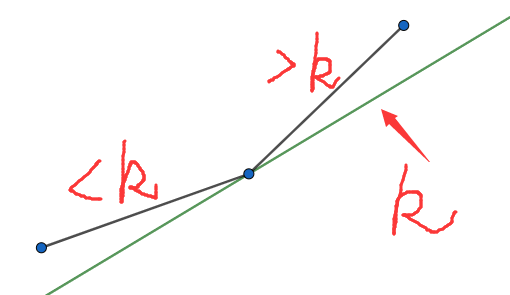
这样我们只要在凸壳上找到这样的一个分界点即可。怎么找呢？不难发现斜率 $T_i + S$ 是单调递增的，所以在凸壳上这个分界点一定是逐渐右移的，像这样：

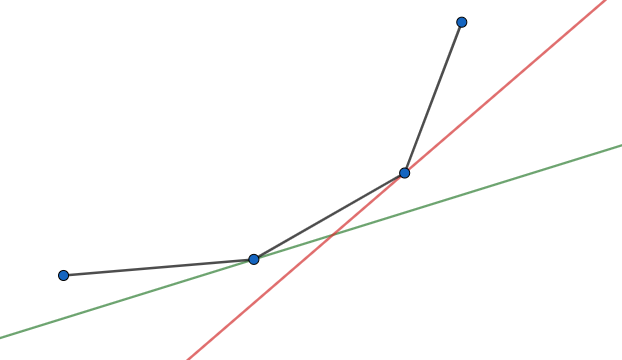
绿线是前一次转移，红线是当前转移，可以看见斜率增加，分界点向右移动。所以我们可以只保存凸壳上斜率大于$T_i + S$ 的部分，就可以快速转移。最后只剩下一个问题，就是维护凸壳。这个也很简单，每次尝试在右侧加入点 $X_i, Y_i​$ 判断与前一个点连边斜率是否大于前一条边，即是否满足下凸壳的性质，大于的话就把凸壳的 右端点删除，继续尝试。就是这样一个过程：

尝试加入这个点，发现不满足下凸壳性质，因此删掉右端点：

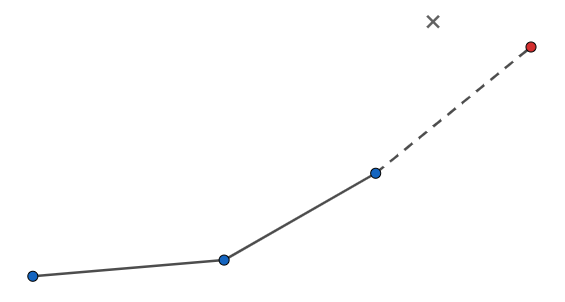
发现满足，这个点就成功加入了。

然后你就会发现双端队列可以很好地满足我们维护凸壳的需求。

这样就可以做到 $\Theta(n)$ 了。斜率优化的大致思想就是这样吧。

CODE

#include <bits/stdc++.h>
using namespace std;
#define N 300010
#define eps 1e-6
#define int long long

int n, S, c[N], t[N], q[N], l, r, f[N];
// q 就是维护凸壳的队列

signed main() {
    scanf("%lld%lld", &n, &S);
    for (int i = 1, tt, cc; i <= n; i ++) {
        scanf("%lld%lld", &tt, &cc);
        c[i] = c[i - 1] + cc; // 前缀和
        t[i] = t[i - 1] + tt;
    }
    memset(f, 0x3f, sizeof f), f[0] = 0, l = r = 1, q[1] = 0;
    for (int i = 1; i <= n; i ++) {
        while (l < r) { // 将斜率大于当前值的删去
            double k = 1.0 * (f[q[l]] - f[q[l + 1]]) / (c[q[l]] - c[q[l + 1]]);
            /*注意这里以及下面都使用了 double 存储斜率来方便理解，
            一般要将除法运算转换成乘法来提高精度，但这样也是可以 A 的 Qwq*/
            if (k - (t[i] + S) > eps) break;
            l ++;
        }
        f[i] = f[q[l]] + t[i] * (c[i] - c[q[l]]) + (c[n] - c[q[l]]) * S; // 转移
        while (l < r) { // 维护凸壳
            double k1 = 1.0 * (f[q[r]] - f[q[r - 1]]) / (c[q[r]] - c[q[r - 1]]);
            double k2 = 1.0 * (f[i] - f[q[r]]) / (c[i] - c[q[r]]);
            if (k2 - k1 > eps) break;
            r --;
        }
        q[++ r] = i; // 插入新点
    }
    printf("%lld\n", f[n]);
    return 0;
}
/* 完结撒花！ */